材料的微观结构决定了其宏观性质,这意味着通过调整材料内部的原子构型可以实现所期望的输运性质。而当材料中存在杂质时,输运对应的“波”将可能被局域化,从而阻碍其相关载流子的输运。1958年P. W. Anderson提出了著名的电子局域化理论,该研究激发了在相关领域中对局域化的广泛研究,围绕着多体局域化和本征态热化的研究已然成为了现代物理学的前沿课题之一。由于自然界中波存在的普遍性,人们在晶格热输运中也观察到了声子的局域化现象。Matsuda和Ishii在1970年的文献中指出,在一维质量无序简谐晶格中低频声子的局域化长度为:
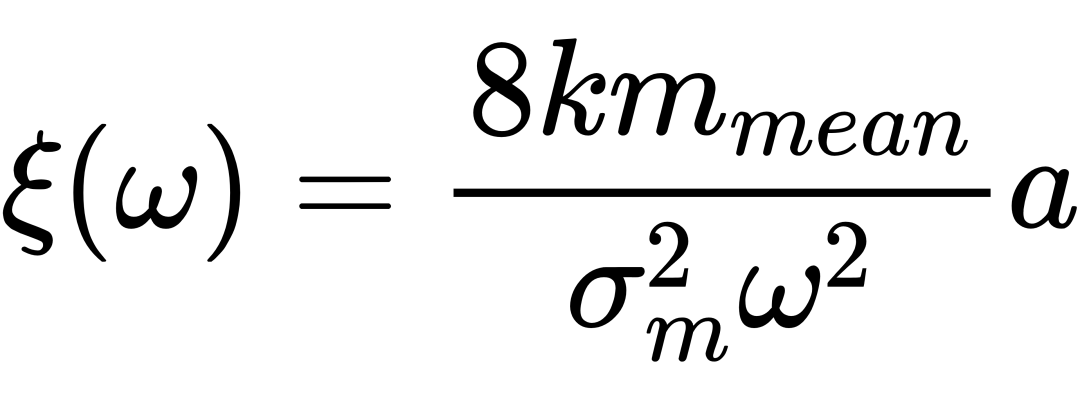
但无序如何影响各频率声子对热传导的贡献迄今尚未得到充分理解。
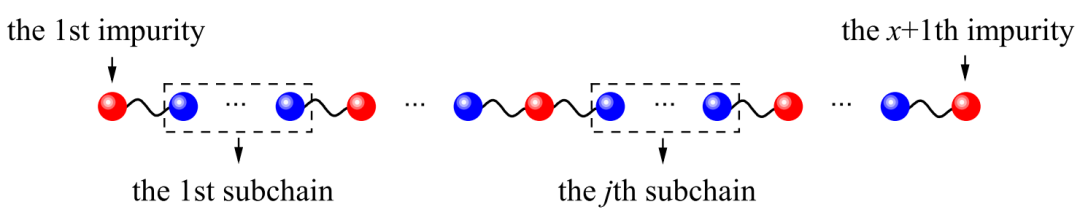
图1. 一维无序双原子简谐链的简化示意图。此无序系统可视为x+1个杂质间夹杂 x 段均匀链,其中第 j 段均匀链含有 aj 个均匀粒子。
最近,厦门大学物理科学与技术学院贺达海课题组基于朗之万格林函数法(LEGF)进行热流谱分解,发现在一维简谐晶格中掺入杂质(图1)可导致声子的平均传输函数(transmission)在特定频率处存在毛刺(spike)(图2),其产生机制来源于杂质将均匀晶格分为多段长度随机的子链(图1)。朗之万格林函数法指出,简谐链的传输函数由粒子间的转移矩阵乘积决定,转移矩阵包含粒子质量、弹性系数和声子频率等参数。由于在特定频率处子链的转移矩阵乘积的种类数有限,导致平均传输函数不同于该频率的邻域。平均传输函数在特定频率处具有的凸起或凹陷称为“毛刺”。子链传输函数在特定频率下的取值种类数越少,则毛刺越明显。
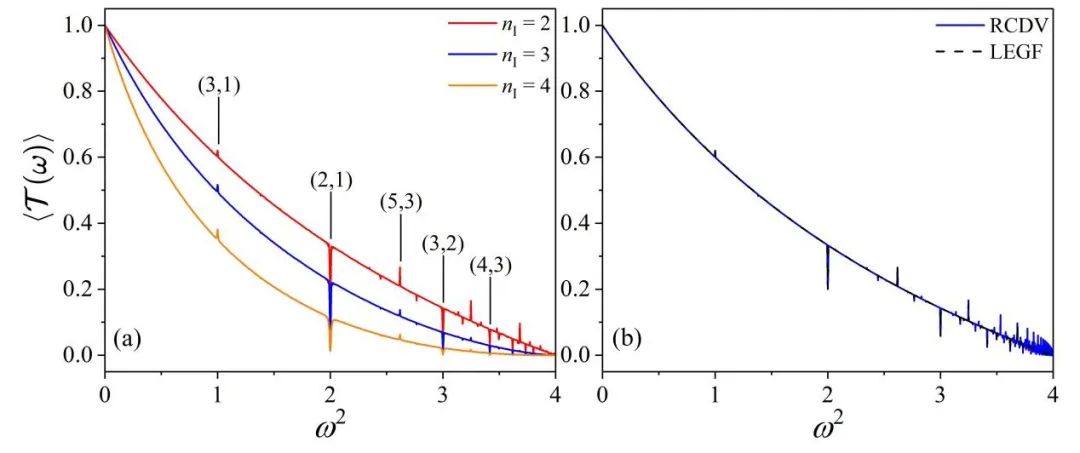
图2. 一维无序双原子链声子传输函数的毛刺现象。(a) 不同杂质个数下系统的传输函数。(b) RCDV方法得到的传输函数与传统LEGF方法对比。
值得注意的是,毛刺对应的频率稠密分布于色散关系允许的声子频带中,该频率可由有序数对 (n, l) 给出(图2)。当杂质将晶格分为 x 段子链时,每段子链的转移矩阵乘积在 ωn,l 频率下有 n 种取值,考虑到非回文且互为对称的晶格(如“121”为回文序列,“112”与“211”为一对非回文对称序列)具有相同的传输函数,可知该频率下晶格整体的传输函数 T(ωn,l) 的取值种类数 nc 满足:当 x=1 时 nc=n,当 x=2 时 nc=n(n+1)/2,当 x>2 时 nc≈nx/2。
利用上述结论,他们提出了构型聚类与离散值(RCDV)方法,用以计算热力学极限下无序简谐晶格的平均传输函数。该方法指出在热力学极限下无穷多种构型的平均传输函数等价于 nc 种构型的平均传输函数。由于稠密的毛刺可构成平均传输函数,按毛刺的明显程度将频率排序得到 ω1,l, ω2,l, ... 序列后,通过Eq. (2)逐一求出离散的平均传输函数,直到频率间隔小于设定的阈值即可得到近似连续的平均传输函数。
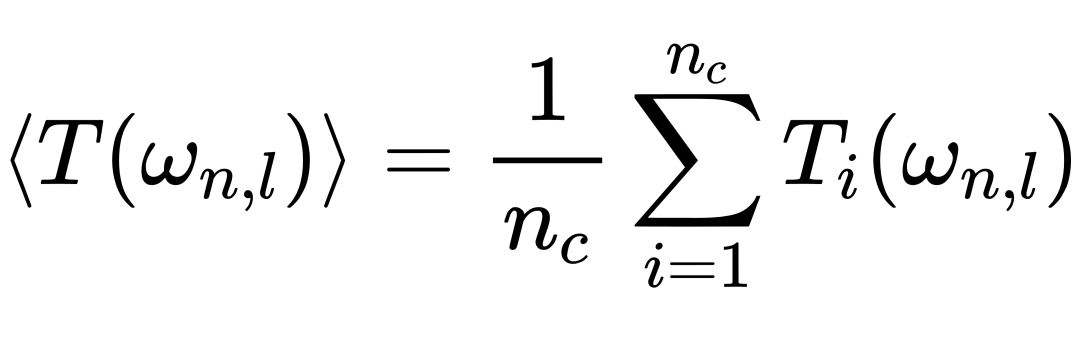
另一方面,他们发现了在无序简谐晶格的平均对数传输函数中忽略毛刺可得平滑基准线,其解析式正比于杂质数,因此可由单杂质晶格的对数传输函数得到多杂质晶格的基准线解析式:
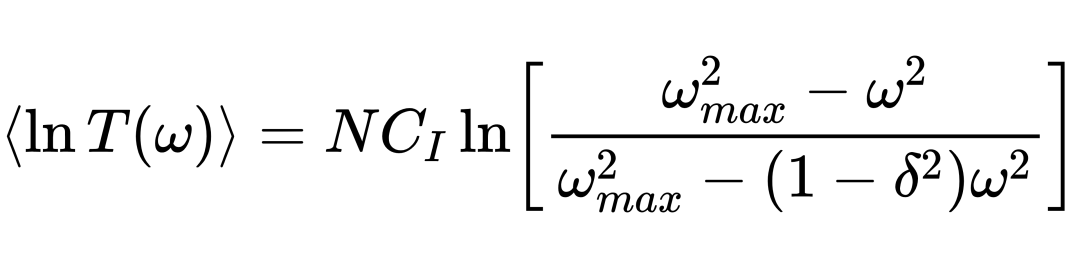
进一步地,对Eq. (3)泰勒展开可得到低频声子局域化长度的表达式Eq. (4),
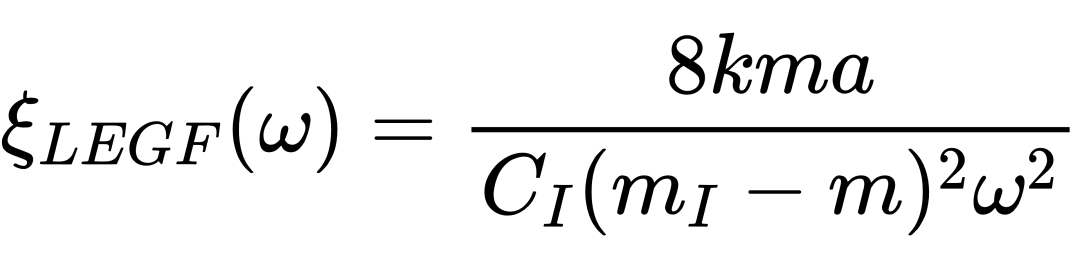
将其与Eq.(1)对比证实了在低杂质浓度下空间无序和质量无序的等价性(图3)。
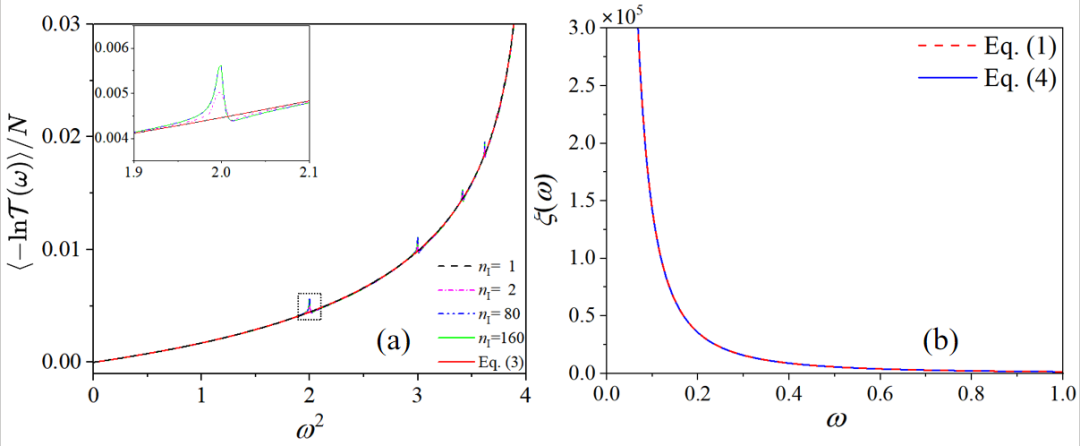
图3. (a) 声子平均对数传输函数的基准线解析式(Eq.3);(b) 低杂质浓度质量无序(Eq.1)和空间无序(Eq.4)的对比。
该工作探索了杂质对简谐晶格声子传输函数的影响,给出了热力学极限下的平均传输函数算法,为进一步理解无序晶格声子输运的物理机制提供了新的思路。相关研究成果以“Disorder-induced spiky phonon transmission of harmonic lattices”为题发表在物理学主流期刊PHYSICAL REVIEW E上(DOI: https://doi.org/10.1103/PhysRevE.109.024129)。研究生林路及博士生魏宇航为论文共同第一作者,厦门大学贺达海教授为论文通讯作者,厦门大学物理学系为第一单位。