关键词：分数量子霍尔效应; 超流体; K矩阵; 玻色-费米;

分数量子霍尔效应一直是最近几十年凝聚态物理强关联研究的重点之一，它的出现不能用经典的朗道的对称性破缺理论解释，推动了凝聚态物理学对于新的物质形态和量子材料的探索，比如超越朗道理论的拓扑序等，掀开了现代物理学的新篇章[1]，也衍生出两个基本问题：(1) 由于拓扑序不能够用朗道序参数描述，如何表征理解分数量子霍尔效应与传统有序态的相变，也是凝聚态物理学的一个挑战，也激发了关于它们之间相变的临界物理性质的研究兴趣；(2) 在已知的量子多体体系里是否能够找到新型的拓扑序，以及如何对它们进行拓扑表征。

(1) 对于非平庸的分数量子霍尔效应与传统拓扑平庸相之间量子相变，一般地，物理上存在两个可能图像：(a) 不连续的一阶相变，属于物理平庸性质；(b)连续的二阶相变，比如分数量子霍尔效应与平庸Mott绝缘体之间的朗道禁闭相变，这个相变临界点在有效量子场理论QED3上可以通过无能隙的狄拉克费米子与衍生的Chern-Simons规范势之间相互耦合描述。另一方面，最近几年关于拓扑能带的出现也为凝聚态提供了全新的思路，在不加磁场时，Haldane提出时间反演对称性破缺的六方晶格拓扑能带模型，这些反常量子霍尔拓扑态出现于分数化能带填充的相互作用多体体系，定性上有别于传统分数量子霍尔效应，在这些系统中，如何描述类似的相变也在近期引起了国际凝聚态物理学界的研究热情与广泛关注。

今年初，厦门大学曾天生课题组的第一个工作是，基于拓扑平带数值分析了分数量子霍尔效应与拓扑平庸的Mott绝缘体、玻色超流凝聚体之间的量子相变。作者证明了在强相互作用下，通过调节格点的周期性化学势大小，可以诱导玻色子Laughlin v=1/2分数量子霍尔效应与玻色子Mott绝缘体之间发生连续量子相变，并对基态简并度、拓扑纠缠熵等量子数的变化，给出连续相变的定量物理描述，与场理论的预言符合；

其次，在弱相互作用下，众所周知玻色子容易发生玻色-爱因斯坦凝聚形成超流体，那么存在的物理问题是在不断调节相互作用时，玻色子Laughlin v=1/2分数量子霍尔效应与超流体会发生什么样的相变。在早期的连续体系有效理论构建中，M. Barkeshli 和J. McGreevy认为在存在空间对称性下，可以发生连续相变[2]。但是在本工作中，作者利用大尺度的严格对角化(ED)和可控精度的密度矩阵重整化群(DMRG)数值计算，定量物理计算却给出了平庸的一阶相变性质(见图1所示)，这也从另一个角度说明拓扑序与传统朗道量子相之间相变的复杂性，依旧值得更多理论的探索。

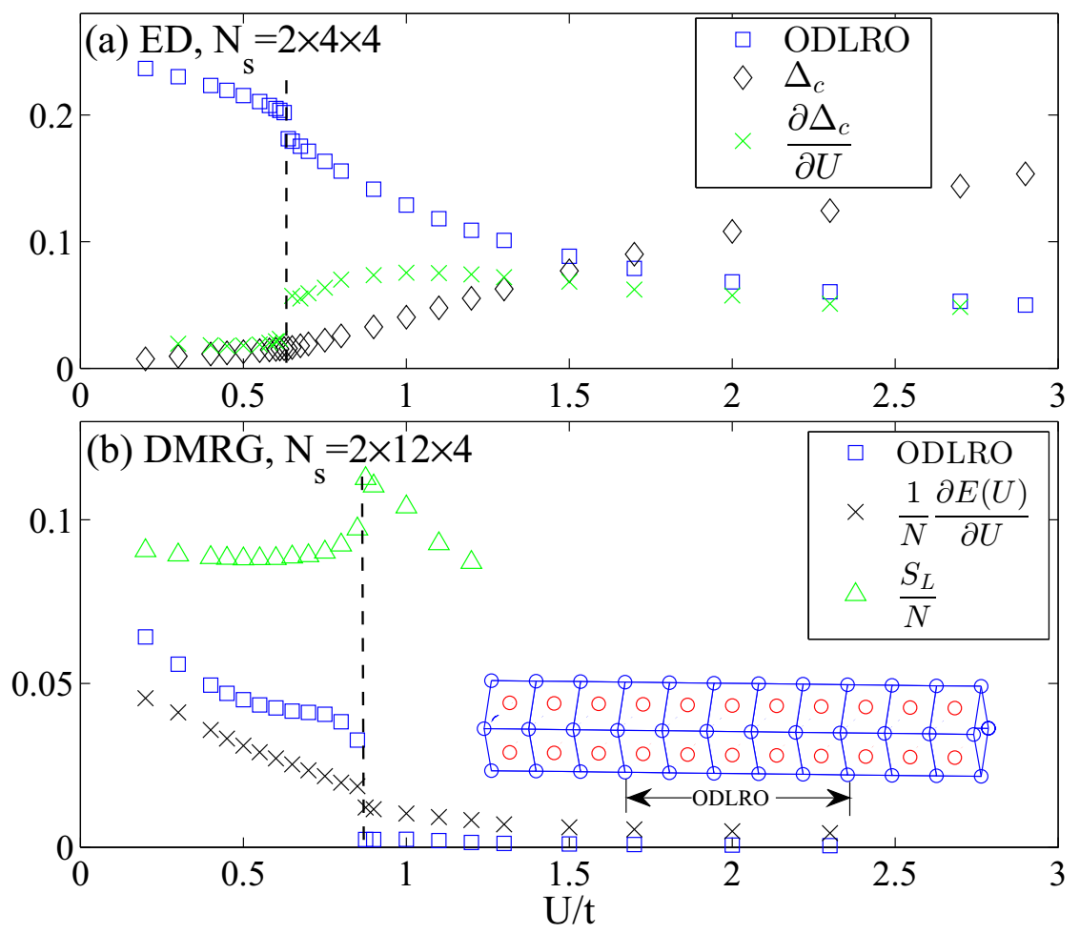
图1 玻色Laughlin v=1/2分数量子霍尔效应与玻色子凝聚体之间的不连续一阶相变(ODLRO代表非对角元长程序，在强相互作用U/t>>1时是分数量子霍尔效应，在弱相互作用U/t<1时是玻色凝聚体)

(2) 对于新型拓扑序，吸引了众多理论工作者思考的问题是：在拓扑能带上是否存在更多新型未知的阿贝尔型多组分分数量子霍尔效应态？2014年实验上在周期性驱动的光晶格中得到了拓扑的Haldane六方蜂窝晶格，包括两组分的费米子气体之间高度可调节的Hubbard相互作用，也为基于拓扑平带实现新奇分数量子霍尔效应提供强有力的探索平台[3]，以及2019年石墨烯双层霍尔系统中观测到新型的多组分分数量子霍尔效应，打开了探索多组分拓扑序的大门[4]。与单组分系统有很大的不同，对于多组分霍尔效应的探索将进一步加深对于拓扑物态的认知，这里不同组分之间的相互作用耦合可以出现全新的拓扑量子相，存在于高陈数的拓扑平带和石墨烯双层等新兴领域。因此，新型的多组分分数量子霍尔效应的发现不仅对也必将大大加深了我们对量子多体系统的理解，同时为寻找相关拓扑性质的材料提供基础。

图二 玻色-费米混合物的量子多体哈密顿量模型(b代表玻色子，f代表费米子)

在第二个工作中，曾天生课题组构建设计了拓扑平带上多组分体系哈密顿量里不同组分之间的二体相互作用(见图2所示)，通过数值计算去寻找拓扑平带中在不同相互作用下量子多体系统可能出现的阿贝尔型多组分分数量子霍尔效应态。作者基于严格对角化和大尺度可控精度的重整化群方法研究了新型多组分分数量子霍尔效应，比如两组分的玻色-费米混合物，首先通过严格对角化分析基态拓扑简并度(=K矩阵的行列式值)，去计算基态多体波函数的分数量化的陈数(Chern number)矩阵(=K矩阵的逆矩阵)，其次通过密度矩阵重整化群分析波函数的分数化电荷泵浦(包括不同组分之间负向的拖拽霍尔电导和同组分之间正向的霍尔电导，见图3所示)、纠缠谱(两支边界态的运动方向、能谱计数)和拓扑纠缠熵(见图4所示)，从而证明它们的K矩阵拓扑性质。进一步构建设计拓扑平带上多组分体系哈密顿量里不同组分之间的三体相互作用，通过数值模拟去寻找可能出现的两组分非阿贝尔型自旋单态分数量子霍尔态，发展刻画非阿贝尔型拓扑序的陈数矩阵的数值计算方法。

图3. 在其中一个组分插入磁通θ变化的分数化电荷泵浦，包括不同组分之间负向的拖拽霍尔电导(Drag Hall condutance)和同组分之间正向的霍尔电导。

图4.基态纠缠谱的能谱计数1、2、5、10、…等(对应于Luttinger边界态激发能谱,传播方向与K矩阵的本征值的正负号一致);右边蓝色小图展示了纠缠熵随着体系尺寸Ny变化的线性拟合S(Ny)=α Ny - γ(γ代表拓扑纠缠熵= K矩阵的行列式值的开根号)。

两个相关成果分别以“Phase transitions of bosonic fractional quantum Hall effect in topological flat bands”为题以regular长文形式，和以“Fractional quantum Hall effect of Bose-Fermi mixtures”为题以Letter短文形式快速发表在美国APS杂志Physical Review B上( Phys. Rev. B 103, 085122 (2021)；Phys. Rev. B 103, L201118 (2021) )。厦门大学曾天生副教授是论文的唯一作者兼通讯作者。该工作得到了国家自然科学基金面上项目(项目号12074320)的支持。

文章链接

1

https://journals.aps.org/prb/abstract/10.1103/PhysRevB.103.085122

2

https://journals.aps.org/prb/abstract/10.1103/PhysRevB.103.L201118

参考文献：

[1] X. G. Wen, “Zoo of quantum-topological phases of matter”, Rev. Mod. Phys. 89, 41004 (2017).

[2] M. Barkeshli and J. McGreevy, “Continuous transition between fractional quantum Hall and superfluid states”, Phys. Rev. B 89, 235116 (2014).

[3] G. Jotzu, M. Messer, R. Desbuquois, et al, “Experimental realization of the topological Haldane model with ultracold fermions”, Nature 515, 237-240 (2014).

[4] X. Liu, Z. Hao, K. Watanabe, et al, “Interlayer fractional quantum Hall effect in a coupled graphene double layer”, Nature Physics 15, 893 (2019).